Momentos Flexionantes - II

la fuerza cortante que se dio con anterioridad en la figura 6-19 también se muestra

Momentos Flexionantes - I

Los momentos flexioantes, además de las fuerzas cortantes, se desarrollan en vigas por aplicación de cargas perpendiculares a la viga. 

Estos momentos flexionantes son los que hacen que la viga asuma su figura característica curvada o flexionada . cuando se ejerce presión a la mitad de una vara esbelta, como por ejemplo una regla con apoyo en sus extremos, se tiene una ilustración de lo interior 

 La determinación de la magnitud de los momentos flexionantes en una viga es otra aplicación del principio de equilibrio estático. En la sección anterior, se analizaron las fuerzas en la dirección vertical con el objetivo de determinar las fuerzas cortantes en la viga que han de desarrollarse para mantener todas las partes de la viga en equilibrio. 

 La figura 6-26 muestra una viga simplemente apoyada con una carga concentrada en el centro Toda lavigaesrá en equilibrio lo mismo que cualquier parte de el la Kxarmnc los diagramas de cuerpo libre que se muestran en las partes ib), (c),

Diagramas de fuerza cortante para cargas distribuidas. - II

Diagramas de fuerza cortante para cargas distribuidas. - I

La variación de la fuerza cortante con la posición en la viga que se somete a cargas distribuidas es diferente de la de vigas sometidas a cargas concentradas. El método del diagrama de cuerpo libre sirve para visualizar tales variaciones. Considérese la viga que aparece en la figura 6-23, sometida a una carga distribuida uniformemente de 1500 N/rn en una parte de su longitud. Se desea determinar la magnitud de l¡i fuerza cortante en varios puntos de la viga para dibujar un diagrama de fuer/j

Ejemplo Resultado

Ejemplo

Trace el diagrama de fuerza completo de la viga expuesta

Diagramas de fuerza cortante - I

Conviene los valores de la fuerza cortante contra su posición en la viga como se muestra en la figura 6-20. Tal gráfica se llama diagrama de fuerza cortante y lo que sigue es un análisis del método para crearlo. También se establece las reglas generales para trazar el diagrama de cualquier viga que sólo se somete a cargas concentradas normales.

FUERZAS CORTANTES - III

FUERZAS CORTANTES - II

Un segmentó se forma o I cortar la viga en un punto de interés y al considerar la parte de la viga a un fado del corte Normalmente, se considera que el segmento de interés es el de la izquierda del corte, como se muestra en la figura 6-!')(a) cuya longitudes de 0.5 m. Por tanto, para que el segmento esté en equilibrio, en general, debe haber una fuerza interna que actúa perpendicular al eje de la viga en el corte. En esle caso, la fuerza interna debe ser de 500 N con dirección hacia abajo, Esta es la fuerza cortante y se usará el símbolo V para denotarla. Es decir, t r 50Q N. liste proceso para determinar fuerzas cortantes se puede generalizar enunciando la regla siguiente:

FUERZAS CORTANTES - I

Más adelante se verá que las dos clases de esfuerzos que se desarrollan en una viga snn esfuerces cortantes y esfuerzos flcxioxiantcs. Para calcularlos, se requiere conocer |¿i magnitud de las fuerzas cortantes y los momentos flexionantesen todos los puntos de la \ i^a. Por consiguiente, aunque posiblemente aim no se comprenda el uso final de estas factores. es ncccsan o aprender cómo se delcrmi na la vari ación de I as fuerzas cortantes y los momentos flex tañantes en vigas con muchos tipos tte cargas y combinaciones de apoyos. Las fuerzas corlantes se definen como sigue: 

Las fuerzas cortantes son fuerzas internas que se generan en el material de una viga para equilibrar las fuerzas aplicadas externamente y para garantizar el equilibrio en todas sus partes. 

La presencia de fuerzas cortantes se puede visualizar considerando cualquier segmento de la viga como un cuerpo libre con todas las cargas externas aplicadas. La figura 6-19 muestra un ejemplo. La viga en conjunto está en equilibrio bajo la acción de las reacciones de 50f> N en los apoyos. Y, cualquier segmento de la viga también debe estar en equilibrio.

Ejemplo 2

Calcule las reacciones en la viga saliente figura 6-17

Ejemplo 1

La figura 6-15 muestra el diagrama de cuerpo libre de viga que soporta tubos, y que en su forma original ilustra figura 6-1 calcule las reacciones en las varillas de apoyo

APOYOS DE VIGAS Y REACCIONES EN LOS APOYOS

EI primer paso en el análisis de una viga por lo que se refiere a su seguridad bajo un patrón de carga dado es mostrar en su totalidad las cargas y las reacciones en los apoyos en un diagrama de cuerpo libre, Es muy importante que se puedan tra?ar los diagramas de cuerpo tibrcconbaseen la i lusl ración o descripción física de la viga con carga Esto es lo que se hizo en cada uno de los casos expuestos en las figuras desde 6-1 a 6-14. Después de dibujar el d i agrama de cuerpo libre, es preciso calcular la magnitud de todas las reacciones en los apoyos. Se presume que los métodos usados para hallar las reacciones ya se estudiaron con anterioridad. Por consiguiente, sólo se dan unos pocos ejemplos como repaso y como ilustración de las técnicas que se api ican en este I ibro Se recomienda el siguiente procedimiento general para determinar las reacciones en vigas simples o salientes.

Tipos de vigas - IV

Viga compuesta si bien las vigas compuestas hasta ahora era miembros rectos simples se emplearán el termino viga compuesta para referirse a una integrada por dos o mas piezas que se extienden en diferentes direcciones. La figuras 6-7y 6-8 son ejemplos. Las vigas de este tipo, por lo general, se analizan por partes para determinar las fuerzas cortantes y los momentos flexionantes internos que actúan a lo largo de ellas. A menudo, el lugar donde una pieza se une a otra es un punto crítico de interés 

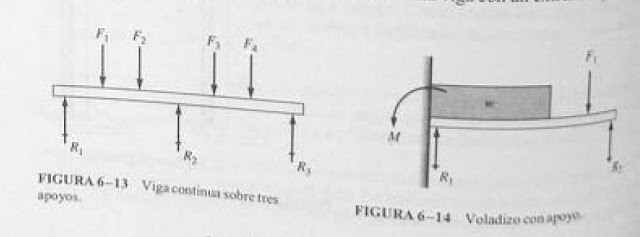
  Vigas continuas A excepción de las vigas que exhiben las partes c y d de la figura 6-10, las vigas abalizadas con anterioridad contaban con uno o dos apoyos y sólo dos reacciones desconocidas. Los principios de la estática permiten calcular todas las fuerzas y momentos de reacción con las ecuaciones de equilibrio clásicas porque hay dos incógnitas y do ecuaciones independientes disponibles con las cuales se pueden determinar las incógnitas

Tipos de vigas - III

Viga en voladizo 
Una viga en voladizo sólo tiene un extremo con apoyo, como se ve en la figura 6-12, que tiene una pluma de grúa finalmente unida a una columna vertical rígida. Es esencial que el apoyo esté fijo porque debe servir de apoyo vertical para las cargas que externamente se aplicaron junto a un momento de reacción opuesto al memento que se produjo por las cargas. Las figuras 6-5 y 6-10ª son otros ejemplos de vigas de voladizo

Tipos de vigas - II

Viga saliente 

una viga saliente es aquella en la que la viga con carga sobresale de los apoyos. La figura 6-11 da un ejemplo. Las cargas que actúan en los extremos salientes tienden a flexionarlos hacia abajo, o sea, a producirles una flexión negativa.

Tipos de vigas - I

El tipo de viga se determina por los tipos de apoyos y su colocación. 

Viga simple 

Una viga simple es la que soporta sólo cargas que actúan perpendiculares a su eje y que tiene sus extremos sobre apoyos simples que actúan perpendiculares a su eje. La figura 6-10 es un ejemplo de viga simple. Cuando todas las cargas actúan con dirección hacia bajo, la viga adopta la figura flexionada clásica cóncava hacia arriba. Esta se conoce como flexión positiva

Tipos de apoyos - III

Apoyo fijo o empotrado 

Un apoyo fijo es el que se mantiene sujeto con firme/a de tul manera que resiste fuerzas en cualquier dirección y también impide la rotación delata en el apoyo. 

Una manera de crear un apoyo fijo es producir una cavidad de ajaste apretado en una estructura rígida en la que se inserta el extremo de mía viga. El apoyo fijo resiste momentos lo mismo que fuerzas porque impide la rotación. La figura 6-10 muestran dos ejemplos del uso de apoyos fijos

Tipos de apoyos - II

Apoyo de pasador 

Un ejemplo de apoyo de pasador es una bisagra que puede resistir en dos direcciones pero que permite rotación con respecto al eje de su pasador. La figura 6-9 b. muestra la misma viga de la figura 6-9ª cib ek rodillo del extremo izquierdo que se reemplazó por una apoyo de pasador. Este sistema produce un apoyo adecuado al mismo tiempo que deja que la viga se flexione. Cualquier fuerza horizontal la resistencia la junta de pasador.

Tipos de apoyos - I

Todas las vigas han de tener un apoyo de una manera eslable para que se mantengan en equilibrio. Todas las cargas y momentos externos deben ser resistidos por uno o más apoyos- Los di ferenlcs t ¡pos de apoyos ofrecen di ferentes tipos de reacciones. 

Apoya simple o de rodillo Un apoyo simple es uno que puedo resistir sólo fuerzas que actúan perpendiculares a una viga.

Una de las mejores ilustraciones de los apoyos simples es el par de rodillo teóricamente libres de fricción en los extremos dela viga según la figura 6-9. Generan apoyo dirigido hacia arriba contra la acción dirigida hacia debajo de la carga que actúa en la viga. Conforme la viga tiende a flexioanerse por la influencia de la carga aplicada y de las reacciones, la flexión no la resistirían los rodillos, pero si hubiera componentes horizontales de la carga, los rodillos rodarían y la viga estaría suelta. Por consiguiente, el uso de los dos rodillo solos no es conveniente.

Momentos concentrados

Un momento es una acción que tiende a hacer girar un objetivo. Los momentos pueden prodcirse por un par de fuerzas paralelas que actúan en direcciones opuestas: esta acción se llama PAR. La acción contra una manivela o una palanca produce un momento

  Cuando un momento actúa en un punto de una viga de manera que tiende a provocarte rotación pura, se llama momento concentrado. 

La figura 6-7 muestra un ejemplo. Las fuerzas que actúan en los extremos de los brazos verticales forman un par que tiende a flexionar la viga como se indica. El hecho de que las dos fuerzas que componen el par sean iguales y opuestas hace que ninguna fuerza horizontal neta resulte aplicada en la viga. Los momentos concentrados también pueden ser el resultado de una fuerza que actua sobre una viga paralela a su eje con su línea de acción a una cierta distancia de éste. Esta situación se ilustra en la figura 6-8 la diferencia en este caso radica en que también hay una fuerza horizontal desbalance aplicada en la viga.

Cagas variables distribuidas

Las cargas de magnitud variable que actúan perpendiculares al eje de una viga a lo largo de un segmento significativo de una viga se llaman cargas variables distribuidas. 

 En las figuras 6-5 y 6-6 se muestra ejemplos de estructuras de cargas variables distribuidas. Cuando las cargas varían linealmente, éstas se cuantifican mediante el valor de en cada extremo de la línea de pendiente que representa la carga. Para un análisis mas fondo de las variaciones no lineales, se deben diseñar otros esquemas para obtener la magnitud de la carga.

Cargas uniformemente distribuidas

Las cargas de magnitud constante que actúan perpendiculares al eje de una viga a lo largo del segmento significativo de la viga se llaman cargas uniformemente distribuidas.

Un ejemplo de este tipo de carga seria el peso de la nueve de espesor uniforme sobre un techo soportado por vigas horizontales planas. Asimismo, los materiales que componen la estructura de techo, propiamente dicha, con frecuencia se instalan uniformemente distribuidos. La figura 6-4 ilustra un patrón de carga de ese tipo de muestra cómo se representa las cargas uniformemente distribuidas en los problemas de este libro. El área rectangular sombreada define la extensión de la carga a lo largo de la viga. La magnitud de la carga se indica por medio de una razón de carga, en unidades de fuerza por unidad de longitud. Las unidades representativas serían lb/plg. kN/m o K/pie Recuérdese que 1K – 1 kip =100lb por ejemplo , si la carga que actúa en la viga mostrada en la figura 6-4 fuera de w=150lb/plg, entonces cada 1.0 plg de longitus de una viga soportaría 150 lb de carga

Cargas concentradas con inclinación

Una carga concentrada inclinada es la que actúa efectivamente en un punto pero cuya línea de acción forma un ángulo con el eje principal de la viga. La figura 6-3 muestra un ejemplo. 

La carga con inclinación y que ejerce es resorte provoca combinación de esfuerzos flexioanantes y axiales en la viga.

Patrones de carga

En esta sección se demostrará que la naturaleza del patrón de carga determina la variación de la fuerza cortante y el momento flexionante a lo largo de la viga. Se definen los cinco patrones de carga más usuales y se dan ejemplos de cada uno. A menudo se pueden analizar patrones de carga más complejos considerandolos como combinaciones de dos o más de los tipos básicos. Cargas concentradas nórmales Una carga normal concentrada es la que actúa perpendicular (normal) al eje mayor de la viga en un solo punto o a lo largo de un segmento muy pequeño de la viga. La figura6-1 (a) muestra I a forma característica de representar una viga que se somete a cargas concentradas normales. Cada una de las cargas se muestra como un vector que actúan en la viga perpendicular a su eje mayor, La parte (B)ilustra una situación que produce cargas concentradas. El peso de los tubos y su contenido determinan las magnitudes de las cargas. Si bien con frecuencia se visualiza cargas que actúan con dirección hacia abajo debido a la gravedad, las cargas reales pueden actuar en cualquier dirección

cargas en Vigas y apoyos y tipos de vigas

Recuerde la definición de viga: una viga es un miembro que se somete a cargas trasversales, es decir, perpendiculares a lo largo de su eje

Cuando se analiza una viga para determinar las reacciones, las fuerzas cortantes internas y los momentos flexionantes internos, conviene clasificar el patrón de carga, el tipo de apoyos el tipo de viga.

Las vigas se someten a varios patrones de carga incluidas

Cargas concentradas normales

Cargas concentradas con inclinación

Cargas uniformemente distribuidas

cargas variables distribución

momentos concentrados

LOS TIPOS DE APOYOS INCLUYEN

Apoyo simple de rodillo

Apoyo pasador

Apoyo fijo o empotrador

Objetivos

La mayor parte del planteamiento en los seis capítulos siguientes se ocupa de las vigas Una viga es un miembro que se somete a cargas transversales, es decir, perpendiculares a lo largo de este eje. Tales cargas provocan esfuerzos cortantes en ID viga y le imparten su figura característica de pandeo, lo que también da como consecuencia esfuerzos flexionantes Para calcular los esfuerzos Cúrtanles y los momentos flexionanles, se precisa determinar la magnitud de \ as fuerzas cortantes internas y los momentos flexionantes que se desarrollan en vigas causados poruña amplia variedad de cargas. Después de terminar el estudia de este capitulo, el lector SCTÍ'Í capaz de: 1, DefínircI ténnino viga y reconocer cuándo un miembro de carga es unaviga 2, Describir varias clases de patrones de carga de vigas: cargas concentradas, cargas uniformemente distribuidas, cargas distribuidas lineal» ten te varia- hles y momentos concentradas. Describir vanas clases de vigas según el tipo de sus apoyos: viga simple »tga saliente, viga en voladizo y vrgw compuesta de más de un componente. 4. Dibujar diagramas de cuerpo libre de vigas y de sus componentes que muo Ucn u>d¡»s l:ts tuerzas y rwiecium^ externas

TORSIÓN EN SECCIONES NO CIRCULARES - IV

Métodos para determinar valores de K y Q de varios tipos de secciones transversales 

TORSIÓN EN SECCIONES NO CIRCULARES - III

TORSIÓN EN SECCIONES NO CIRCULARES - II

En la figura 5-17 se muestra una interesante ilustración de la escasa rigidez ^ perfilesabícitos esbeltos. U placa delgada (a), el ángu lo < b) y el canal (c) 1 ienead m- espesor y área de sección transversal y casi la misma rigidez torsional. Asimismo,«CL, la placa esbelta va a formarse un perfil circular (d) con una abertura, su rigidez ««g^ baja. Sin embargo, si va a cenarse por completo como en la Figura 5-16{a) soWándtfe* estirándolo como los tubos sin costura se tendría un elemento un tanto rígido prensión de estas comparaciones sirve para seleccionar un perfil conveniente par» menins sujetos a torsión.

TORSIÓN EN SECCIONES NO CIRCULARES - I

El comportamiento de secciones no circulares cuando se someten a torsión es diferente en sumo grado del de las secciones circulares* las cuales se estudiaron en éste capítulo. Existe una gran variedad de perfiles y el análisis de su rigidez y resistencia es diferente para cada uno. Hl descolló de las relaciones implicadas no se llevará a cabo aquí. Las recopilaciones de las fórmulas pertinentes se encuentran en las referencias, de la 1 a ta 5, qué aparecen al fina] de este capítulo y en esta sección sedan algunas. Se pueden hacer algunas generalizaciones. las secciones sólidas que tienen !a mis- ma área de sección transversal son más rígidas cuando su forma se aproxima a la de un circulo (véase la figura 5- 14) Por otra parte, un elemento compuesto de perfiles largos esbeltos qii'-- no son cerrados como un tubo son muy débiles y flexibles a torsión. Algunos ejemplos de perfiles flexibles son los perfiles estructurales comunes tales como vigas de patín ancho, vigas 3 estándar, canales, ángulos ytcs,como se ilustra en la figura 5-15 Los tubos, las barras sólidas y los tubos rectangulares estructurales son muy rígidos (véase la figura 5-16).

Ejemplo 3 (Parte 6)

Ejemplo 3 (Parte 5)

por consiguiente

Ejemplo 3 (Parte 4)

Entre D y E en la varilla, el par de torsión es la resultante de todos los pares de torsión que se aplicaron en DC y B

Ejemplo 3 (Parte 3)

En el segmento AB hasta B pero sin que se incluya el disco B, el par de torsión es cero porque la chumacera permite la libre relación. Ahora considere el par de torsión aplicado por el disco B y determine el par torsión en el segmento

Ejemplo 3 (Parte 2)

El primer paso es calcular la magnitud y dirección de los partes de torsión que se aplican a cada disco B,C y D Hágalo ahora recuerde a definición de par de torsión de ecuación

Ejemplo 3 (Parte 1)

La figura 5-11 muestra una varilla de acero con tres discos montados en ella. La varilla tiene su extremo izquierdo fijo contra rotación, pero con el extremo derecho libre para girar sobre una chumacera. Cada disco es de 300 mm de diámetro. En las caras externas de los discos actúan fuerzas dirigidas hacia abajo de modo que la varilla se ve sometida a pares de torsión. Determine el ángulo de torsión de la sección A con respecto a la sección fija E,

Ejemplo 2 - Resultados

Ejemplo 2

determine el diámetro conveniente de una flecha redonda de aleación de aluminio 6061 – T6 si no se debe torcer más de 0.08 grados en 1.0 pie de longitud cuando se aplica un par de torsión de 75 lb.plg

Ejemplo 1

Determine el ángulo de torsión en grados entre dos secciones con una separación de 250 mm en una vanill a de acero de 10 mm de diámetro cuando se aplica un par de torsión de 15 Nm

TORSIÓN-DEFORMACIÓN TORSIONAL ELÁSTICA - IV

F,1 ángulo de torsión resáltame, 0. está en radianes. Cuando en el calculóse útil izan unida- des compatibles para todos los términos, todas las unidades se eliminan y queda un núme- ro adimensional. Éste, puede interpretarse corno ct ángulo, 0, en radianes. La ecuación (5-22) puede usarse para calcular el ángulo de torsión de una sección de una barra circular, ya sea sólida o hueca, con respecto a otra donde l es la distancia entre el las, siempre que el par de torsión Tr el momento polar de inercia y el módulo de elasticidad a córtame, G, sean los mismos a lo largo de L. Si alguno de estos factores varia en un problema dado, la barra puede subdividuse en segmentos donde sean cons- tantes para calcular ángulos de rotación de tales segmentos. Luego los ángulos que se calcularon se pueden combinar algebraicamente para obtener el ángulo total de torsión. Este principio, llamado s^terpóstetón, se ilustrará por medio de ejemplos. El módulo de elasticidad acortante, G„ mide la rigidez torsional del material de la barra. La tabla 5-3 da valores de G para materiales que se seleccionaron.

TORSIÓN-DEFORMACIÓN TORSIONAL ELÁSTICA - III

En la superficie externa por consiguiente

TORSIÓN-DEFORMACIÓN TORSIONAL ELÁSTICA - II

bros circulares, tanto sólidos como huecos, Los perfiles no c i reularcs se cuudjarin^ adelante. Esmuy importante señalar que el comportamiento de un perfil ato i crióla] ^ un canal o ángulo es muy diferente del de un perfil cerrado tal como un tubocm^, rectangular En general, los perfiles abiertos tienen una rigidez torsional muy bnJa Como una ayuda en el desarrollo de la relación para calcular el ángulo de lorsn» un miembro circular, considérese la flecha que ilustra Ja figura 5-3. Uno de sus ex:^ se mantiene fijo mientras se aplica un par de torsión 7* al otro. En estas condicionak tlecha se torcera entre los dos extremos a través de un ángulo 0, 

La derivación de la fórmula para el ángulo de torsión depende de algunas súpose• eiones básicas con respecto al comportamiento de un miembro circular que se sometía torsión. Conforme se aplica el par de torsiónr un elemento a lo largo de la superficie extema del miembro, iniciahiicnte recto, gira un pequeño ángulo /{gamma). Asunta un radio del miembro en una sección transversal gira en un pequeño ángulo 0. En la figu 5-3, las rotaciones yyO guardan relación con la longitud del arco AB en la superficie la barra. Por la geometría > para ángulos pequeños, la lortgiiud del arco es el produelo dd ángulo en radianes y d radio medido a partir del centro de rotación, Por consiguiera, J longii ud del arco Ali puede expresarse como;

TORSIÓN-DEFORMACIÓN TORSIONAL ELÁSTICA - I

La rigidez además de la resistencia es una impórtame consideración de diseño de miembros sujetos a torsión La medida de la rigidez Doreional es el ángulo de torsión de un segmento de una flecha con respecto a otro cuando se aplica un cierto par de torsión. 

En aplicaciones de transmisión de potencia mecánica, la excesiva torsión de una flecha puede provocar problemas de vibración que, a su vez, pueden provocar rwidoy una sincronización impropia de las piezas móviles. 

Lina indicación por loqtte.se refiero a rigidez torsional tiene qué ver con el grado de precisión qtte se desea, como se indica en I a tabla 5 2 (vean se las re ferenc i as 3 y 3). Kn el diseño estructural, lus miembros de carga en ocasiones se someten a torsión así como también a leu sióri o flexión. La rigidez; de una estructura depende entorices de la rigidez torsional de sus componentes. Cualquiercaqpaplicada fuera del eje de un miembro v transversal al mismo producirá torsión, l isia sección analizará la torsión de miembro

Ejemplo

Se muestra un segmento de una flecha en la que se maquinó una ranura circular. Para un par de torsión aplicado de 4500 lb.plg calcule es esfuerzo cortaría torsional en la sección 1, donde el diámetro es máximo, y en la sección 2, donde la localiza la ranura

Flechas con cuñeros.

Los elementos transmisores de potencia por lo general irans^ miten un par de torsión hacia y desde las flechas por medio de cuñas que se insertan en cuñeros en la flecha como se muestra en la figura 5-9, La polea de banda en V montada en el extremo de la flecha motriz constituye un ejemplo, tíos tipos de cuñeros son los de uso más frecuente: los cuñeros de extremo y losdc perfil. Pura cortar el cunero de ex tremo, por lo general en el extremo de una Hecha, se usa una fresa circular de espesor igual al ancho del cunero, como se muestra en la figura 5 -9(b). 

Al filial del corte, ta fresa deja un t Lidio pequeño, como se ilustra en la vista lateral, que da K, 1.6 como valor de diseño. Un cuñero de perfil se corta cor» una fresadora escariador» de diámetro igual al ancho del c uñero. 

Cortado, por lo general, en un lugar distantea los extremos de la (lecha, deja esquinas interiores a escuadra en los extremos del cu ñero visto de lado, como se muestra en la figura 5~9(c), Lstc es más severo que el cu ñero de extremo y se usa un valor de K, 2.0. Nótesequc los factores de concentración de esfuerzo tienen en cuenta tanto la remoción de material de la flecha como el cambio de geometría

Barra redonda escalonada.

Las flechas con frecuencia se fabrican con dos o mis diámetros, lo que da por resultado una flecha escalonada como la que se muestra en el apéndice A-21 -7. La cara del escalón sirve para localizar un lado de un elemento que se monta en la flecha, tal como un cojinete, engrane, polca o una nieda dentada para cadena. Se debe tener cuidado al definir el radio de la base del escalón, llamado radio de redon- deo. Deben evitarse los vért ices puntiagudos, porque provocan factores de concentración de esluerzo muy elevados. Bl radio ha de ser tan grande como sea posible y al mismo tiempo compatible con los elementos montados en la flecha. Los anillos dc retención que se asientan en las ranuras cortadas en la flecha, a menudo se usan para localizar elementos de máquina, como se muestra en la figura 5-8. Las ranuras por lo general son dc fondo plano con radios pequeños en los costados. Algunos diseñadores tratan a tal es ranuras como si fueran dos escalones muy juntos en la flecha y utilizan la gráfica de flechas escalonadas (apéndice A-2l-7)para determinar el factor de concentración de esfuerzo. Por el radio pequeño en la base de la ranura, el radio relativo con frecuencia es bastante pequeño, lo eual resulta en que se tomen valores elevados de K, de la gráfica. En tales casos, suele usarse un valor de K¡=3.0.

Barra redonda ranurada.

Las ranuras de fondo redondeado se cortan en las barras redondas con el objeto de instalar sellos o para distribuir aceite lubricante alrededor de una flecha. 1,1 factor de concentración de esfuerzo depende de ta relación del diámetro de la flecha al diámetro de la ranura y de la relación del radio de la ranura al diámetro de la misma. La ranura se corta con una herramienta de boca redondeada que produce la ranura de fondo redondeado. El radio ha de ser tan grande como sea posible para reducir at mínimo el factor de concentración de esfuerzo. Nótese que el esfuerzo nominal se basa en e l diámetro en la base de la ranura, Véase el apéndice A-21 -6.

Barra redonda con un agujero transversal - II

El pasador sirve para situar el elemento de maquina axialmente en la flecha al mismo tiempo también trasmite el par de torsión de la flecha al elemento o de éste a la flecha. El agujero en la flecha es un cambio reperntino de geometria y causa una concentracion de esfuerzo. El apéndice A -21-5 es ina gráfica de este caso con la que se puede determinar K, La curva C corresponde al caso del flechas sometidas a torsión . notesé que la formula para el esfuerzo nominal en la flecha se basa en toda la sección transversal circular bruta de la flecha

Barra redonda con un agujero transversal - I

El objeto de perforar u agujero en una flecha es insertar un pasador a través del agujero y a través del agujero correspondiente en la maza de un elemento de máquina tal como un engrane, polea a rueda dentada para cadena

CONCENTRACIONES DE ESFUERZO EN ELEMENTOS SOMETIDOS A TORSIÓN - II

Éste es un segmento dc una Hecha en la que se va a montar un elemento transmisor de potencia como, por ejemplo, un engrane. El diámetro del agujero en la maza del engrane es mi que permite deslizarlo en el extremo derecho de la flecha donde el diámetro de esta es ¡ 1 25 mm. I n el cilífero se inserta una cuna rectangular y habría un cuñero coi iespondi ente ett la maza del engrane para que se deslice sobre la cuña. El engrane se deslizaría entonces de derecha ¡i izquierda hasta que se detuviera contra el hombro de la sección 2 por el incremento en el diámetro de la flecha a D 40 ni m. Para ma ni ene relé ngranc en posición, se inserta una nillo de sujeción en I a ranura de la sección 4. L os cambios de la sección transversal dc un miembro sometido a torsión provocan que el esfuerzo local cerca de los cambios sea mayor que el que se pronosticó mediante el uso de la fórmula para el esfuerzo cortante torsional, El nivel real de esfuerzo en tales casos se determina de manera experimental. En tal caso se determina un factor de concentración (Je esfuerzo que permita que el esfuerzo máximo en diseños similares se calcule con la relación:

CONCENTRACIONES DE ESFUERZO EN ELEMENTOS SOMETIDOS A TORSIÓN - I

Los miembros sometidos a torsión, en especial las flechas trasmisoras de potencia, con frecuencia se fabrican con cambios de geometría en varias posiciones. La figura 5-8