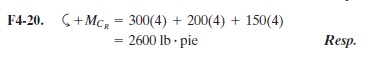Determine las magnitudes de los momentos de par M1, M2 y M3 de modo que el momento de par resultante sea igual a cero.
viernes, 19 de mayo de 2017
jueves, 18 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 24
Si M1 = 180 lb*pie, M2 = 90 lb*pie y M3 = 120 lb*pie, determine la magnitud y los ángulos directores coordenados del momento de par resultante.
miércoles, 17 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 23
Determine la distancia d entre A y B de modo que el momento de par resultante tenga una magnitud MR = 20 N*m.
martes, 16 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 22
Determine el momento de par resultante de los dos pares que actúan sobre el ensamble de tubos. La distancia desde A hasta B es d = 400 mm. Exprese el resultado como un vector cartesiano.
domingo, 14 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 21
Para voltear el bastidor, se aplica un momento de par como el que se muestra en la figura. Si la componente de este momento de par a lo largo del eje x es Mx = {-20i} N*m, determine la magnitud F de las fuerzas de par.
sábado, 13 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 20
Exprese el momento del par que actúa sobre el bastidor en forma de vector cartesiano. Las fuerzas se aplican de manera perpendicular al bastidor. ¿Cuál es la magnitud del momento de par? Considere que F = 50 N.
viernes, 12 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 19
A partir de los cálculos de carga, se ha determinado que el ala está sometida a momentos de par Mx = 17 kip*pie y My = 25 kip*pie. Determine los momentos de par resultantes producidos con respecto a los ejes x´ y y´. Todos los ejes se encuentran en el mismo plano horizontal.
jueves, 11 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 18
Si la magnitud del momento de par que actúa sobre el ensamble de tubos es de 50 N*m, determine la magnitud de las fuerzas de par aplicadas en cada llave. El ensamble de tubos se encuentra en el plano x-y.
miércoles, 10 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 17
Si F = 80 N, determine la magnitud y los ángulos directores coordenados del momento de par. El ensamble de tubos se encuentra en el plano x-y.
martes, 9 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 16
Determine la magnitud requerida de los momentos de par M1, M2 y M3 para que el momento de par resultante sea MR = {300i + 450j - 600k} N*m.
lunes, 8 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 15
Si M1 = 500 N*m, M2 = 600 N*m y M3 = 450 N*m, determine la magnitud y los ángulos directores coordenados del momento de par resultante.
domingo, 7 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 14
Dos pares actúan sobre el bastidor. Si d = 4 pies, determine el momento de par resultante. Para que calcule el resultado descomponga cada fuerza en componentes x y y.
Además obtenga el resultado (a) al determinar el mo mento de cada par (ecuación 4-13) y (b) al sumar los mo men tos de todas las componentes de fuerza con respecto al punto B.
Además obtenga el resultado (a) al determinar el mo mento de cada par (ecuación 4-13) y (b) al sumar los mo men tos de todas las componentes de fuerza con respecto al punto B.
sábado, 6 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 13
Dos pares actúan sobre el bastidor. Si d = 4 pies, determine el momento de par resultante. Para que calcule el resultado descomponga cada fuerza en componentes x y y.
Además obtenga el resultado (a) al determinar el momento de cada par (ecuación 4-13) y (b) al sumar los momentos de todas las componentes de fuerza con respecto al punto A.
Además obtenga el resultado (a) al determinar el momento de cada par (ecuación 4-13) y (b) al sumar los momentos de todas las componentes de fuerza con respecto al punto A.
viernes, 5 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 12
Dos pares actúan sobre la estructura. Si el momento del par resultante debe ser igual a cero, determine la distancia d entre las fuerzas del par de 40 lb.
jueves, 4 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 11
Determine la magnitud requerida de la fuerza F, si el momento del par resultante sobre la viga debe ser igual a cero.
miércoles, 3 de mayo de 2017
martes, 2 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 9
Determine el momento del par resultante que actúa sobre la viga. Resuelva el problema de dos maneras: (a) sume los momentos con respecto al punto O; y (b) sume los momentos con respecto al punto A.
lunes, 1 de mayo de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 8
Dos pares actúan sobre la viga como se muestra en la figura. Determine la magnitud de F de modo que el momento del par resultante sea de 300 lb # pie en sentido contrario al de las manecillas del reloj. ¿En qué punto de la viga actúa el momento del par resultante?
domingo, 30 de abril de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 7
Un dispositivo llamado rolamita se usa de varias maneras para reemplazar el movimiento deslizante por movimiento rodante. Si la banda, que está enrollada entre los rodillos, se encuentra sometida a una tensión de 15 N, determine las fuerzas reactivas N de las placas superior e inferior sobre los rodillos, de modo que el par resultante que actúa sobre los rodillos sea igual a cero.
sábado, 29 de abril de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 6
Determine el momento de par que actúa sobre el ensamble de tubos y exprese el resultado como un vector cartesiano.
viernes, 28 de abril de 2017
jueves, 27 de abril de 2017
miércoles, 26 de abril de 2017
Momento Par - PROBLEMAS FUNDAMENTALES 3
Determine la magnitud de F de modo que el momento de par resultante que actúa sobre la viga sea de 1.5 kN*m en el sentido de las manecillas del reloj.
martes, 25 de abril de 2017
lunes, 24 de abril de 2017
domingo, 23 de abril de 2017
Momento de un par - Ejemplo 4
Reemplace los dos pares que actúan sobre la columna tubular en la figura 4-33a por un momento de par resultante.
sábado, 22 de abril de 2017
Momento de un par - Ejemplo 3
Determine el momento de par que actúa sobre el tubo de la figura 4-32a. El segmento AB está dirigido 30° por debajo del plano x-y.
viernes, 21 de abril de 2017
Momento de un par - Ejemplo 2
Determine la magnitud y la dirección del momento de par que actúa sobre el engrane de la figura 4-31a.
SOLUCIÓN
La solución más fácil requiere descomponer cada fuerza en sus componentes como se muestra en la figura 4-31b. El momento de par puede determinarse al sumar los momentos de estas componentes de fuerza con respecto a cualquier punto, por ejemplo, el centro O del engrane o el punto A. Si consideramos que los momentos con sentido contrario al de las manecillas del reloj son positivos, tenemos
SOLUCIÓN
La solución más fácil requiere descomponer cada fuerza en sus componentes como se muestra en la figura 4-31b. El momento de par puede determinarse al sumar los momentos de estas componentes de fuerza con respecto a cualquier punto, por ejemplo, el centro O del engrane o el punto A. Si consideramos que los momentos con sentido contrario al de las manecillas del reloj son positivos, tenemos
jueves, 20 de abril de 2017
Momento de un par - Ejemplo 1
Determine el momento de par resultante de los tres pares que actúan sobre la placa de la figura 4-30.
miércoles, 19 de abril de 2017
Momento de un par - Puntos importantes
• Un momento de par lo producen dos fuerzas no colineales que son iguales en magnitud pero opuestas en dirección. Su efecto es producir una rotación pura, o una tendencia a girar en una dirección especificada.
• Un momento de par es un vector libre y, como resultado, causa el mismo efecto de rotación sobre un cuerpo independientemente de dónde se aplique al cuerpo.
• El momento de las dos fuerzas de par se puede determinar con respecto a cualquier punto. Por conveniencia, a menudo ese punto se selecciona sobre la línea de acción de una de las fuerzas para eliminar el momento de esta fuerza con respecto al punto.
• Un momento de par es un vector libre y, como resultado, causa el mismo efecto de rotación sobre un cuerpo independientemente de dónde se aplique al cuerpo.
• El momento de las dos fuerzas de par se puede determinar con respecto a cualquier punto. Por conveniencia, a menudo ese punto se selecciona sobre la línea de acción de una de las fuerzas para eliminar el momento de esta fuerza con respecto al punto.
martes, 18 de abril de 2017
Momento de un par - Momento de par resultante.
Como los momentos de par son vectores libres, sus resultantes pueden determinarse mediante la suma
Estos conceptos se ilustran numéricamente en los ejemplos que siguen. En general, los problemas proyectados en dos dimensiones deben resolverse con un análisis escalar puesto que los brazos de momento y las componentes son fáciles de determinar.
lunes, 2 de enero de 2017
Momento de un par - Pares equivalentes
Se dice que dos pares son equivalentes si producen un momento con la misma magnitud y dirección. Por ejemplo, los dos pares mostrados en la figura 4-28 son equivalentes porque cada momento de par tiene una magnitud de M = 30 N(0.4 m) = 40 N(0.3 m) = 12 N # m, y cada uno de ellos está dirigido hacia el plano de la página. Observe que en el segundo caso se requieren fuerzas más grandes para crear el mismo efecto de giro, debido a que las manos están colocadas más cerca una de la otra. Además, si la rueda estuviera conectada al eje en un punto distinto de su centro, ésta giraría de igual forma al aplicar cada uno de los pares porque el par de 12 N # m es un vector libre.
domingo, 1 de enero de 2017
Momento de un par - Formulación vectorial.
El momento de un par puede expresarse también por el vector producto cruz con la ecuación 4-13, es decir,
La aplicación de esta ecuación se recuerda fácilmente si se piensa en tomar los momentos de ambas fuerzas con respecto a un punto que se encuentre sobre la línea de acción de una de las fuerzas. Por ejemplo, si los momentos se toman con respecto al punto A en la figura 4-26, el momento de F es cero con respecto a este punto, y el momento de F se define a partir de la ecuación 4-15. Por lo tanto, en la formulación, r se multiplica vectorialmente por la fuerza F a la cual está dirigida.
La aplicación de esta ecuación se recuerda fácilmente si se piensa en tomar los momentos de ambas fuerzas con respecto a un punto que se encuentre sobre la línea de acción de una de las fuerzas. Por ejemplo, si los momentos se toman con respecto al punto A en la figura 4-26, el momento de F es cero con respecto a este punto, y el momento de F se define a partir de la ecuación 4-15. Por lo tanto, en la formulación, r se multiplica vectorialmente por la fuerza F a la cual está dirigida.
Suscribirse a:
Comentarios (Atom)