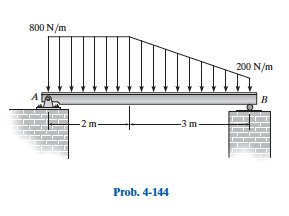
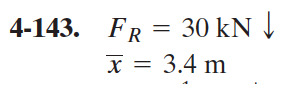4-144. Reemplace la carga distribuida por una fuerza resultante equivalente y especifique su ubicación medida desde el punto A.
viernes, 31 de diciembre de 2021
miércoles, 29 de diciembre de 2021
Reducción de una carga simple distribuida - Problema 2
sábado, 25 de diciembre de 2021
Reducción de una carga simple distribuida - Problema 1
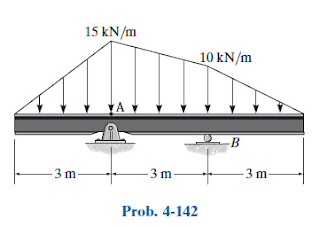
4-142. Reemplace la carga distribuida por una fuerza resultante equivalente y especifique su ubicación sobre la viga, medida desde el punto A.
Respuesta
martes, 21 de diciembre de 2021
Reducción de una carga simple distribuida - Ejemplo 3
El material granular ejerce una carga distribuida sobre la viga como se muestra en la figura 4-51a. Determine la magnitud y la ubicación de la resultante equivalente de esta carga.
jueves, 16 de diciembre de 2021
Reducción de una carga simple distribuida - Ejemplo 2
Una carga distribuida de p = (800x) Pa actúa sobre la superficie superior de la viga que se muestra en la figura 4-50a. Determine la magnitud y la ubicación de la fuerza resultante equivalente.
miércoles, 8 de diciembre de 2021
Reducción de una carga simple distribuida - Ejemplo 1
Determine la magnitud y la ubicación de la fuerza resultante equivalente que actúa sobre la flecha de la figura 4-49a.
miércoles, 1 de diciembre de 2021
Reducción de una carga simple distribuida - Puntos importantes
- Las cargas distribuidas coplanares se definen con una función de carga w = w(x) que indica la intensidad de la carga a lo largo de la longitud del elemento. Esta intensidad se mide en N/m o lb/pie.
- Los efectos externos causados por una carga distribuida coplanar que actúa sobre un cuerpo pueden representarse por medio de una sola fuerza resultante.
- Esta fuerza resultante es equivalente al área bajo el diagrama de carga, y tiene una línea de acción que pasa por el centroide o centro geométrico de esta área.
domingo, 21 de noviembre de 2021
Reducción de una carga simple distribuida - Ubicación de la fuerza resultante
Esta coordenada x, ubica el centro geométrico o centroide del área bajo el diagrama de carga distribuida. En otras palabras, la fuerza resultante tiene una línea de acción que pasa por el centroide C (centro geométrico) del área bajo el diagrama de carga, figura 4-48c. En el capítulo 9 se proporciona un tratamiento detallado de las técnicas de integración para encontrar la ubicación de centroides de áreas. Sin embargo, en muchos casos el diagrama de carga distribuida tiene la forma de un rectángulo, de un triángulo, o algún otro cuerpo geométrico simple. La ubicación de los centroides para formas tan comunes no tiene que determinarse con la ecuación anterior sino que pueden obtenerse directamente de las tablas que aparecen en el forro interior de la contraportada de este libro.
Una vez determinada x, por simetría, FR pasa a través del punto ( x, 0) sobre la superficie de la viga, figura 4-48a. Por lo tanto, en este caso, la fuerza resultante tiene una magnitud igual al volumen bajo la curva de carga p = p(x) y una línea de acción que pasa por el centroide (centro geométrico) de este volumen.
viernes, 19 de noviembre de 2021
Reducción de una carga simple distribuida - Magnitud de la fuerza resultante
A partir de la ecuación 4-17 (FR = ⅀F), la magnitud de FR es equivalente a la suma de todas las fuerzas en el sistema. En este caso, debemos usar integración puesto que hay un número infinito de fuerzas paralelas dF que actúan sobre la viga, figura 4-48b. Como dF actúa sobre un elemento de longitud dx, y w(x) es una fuerza por unidad de longitud, entonces dF = w(x) dx = dA. En otras palabras, la magnitud de dF se determina a partir del área diferencial sombreada dA bajo la curva de carga. Para toda la longitud L.
jueves, 11 de noviembre de 2021
Reducción de una carga simple distribuida - Carga uniforme a lo largo de un solo eje
El tipo más común de carga distribuida que se encuentra en la práctica de la ingeniería es una carga uniforme a lo largo de un solo eje*. Por ejemplo, considere la viga (o placa) de la figura 4-48a que tiene un ancho constante y está sometida a una carga de presión que varía sólo a lo largo del eje x. Esta carga se puede describir mediante la función p = p(x) N>m2. Contiene sólo una variable x, y por esa razón también podemos representarla como una carga distribuida coplanar. Para esto, multiplicamos la función de carga por el ancho b m de la viga, de modo que w(x) = p(x)b N>m, figura 4-48b. Con los métodos de la sección 4.8, podemos reemplazar este sistema de fuerzas paralelas coplanares por una sola fuerza resultante equivalente FR que actúa en una ubicación específica sobre la viga, figura 4-48c.
sábado, 6 de noviembre de 2021
Reducción de una carga simple distribuida
En ocasiones, un cuerpo puede estar sometido a una carga que se encuentra distribuida por toda su superficie. Por ejemplo, la presión del viento sobre la superficie de un señalamiento, la presión del agua dentro de un tanque, o el peso de la arena sobre el piso de un contenedor de almacenaje, son todas cargas distribuidas. La presión ejercida sobre cada punto de la superficie indica la intensidad de la carga. Ésta se mide por pascales Pa (o N/m²) en unidades SI o lb/pie² en el sistema de uso común en Estados Unidos.
lunes, 25 de octubre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 25
•4-141. Reemplace las tres fuerzas que actúan sobre la placa por una llave. Especifique la magnitud de la fuerza y del momento de par para la llave, así como el punto P(x, y) donde su línea de acción interseca la placa.
Respuestas
miércoles, 20 de octubre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 24
4-140. Reemplace las tres fuerzas que actúan sobre la placa por una llave. Especifique la magnitud de la fuerza y del momento de par para la llave, así como el punto P(y, z) donde su línea de acción interseca la placa.
miércoles, 13 de octubre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 23
4-139. Reemplace el sistema de fuerza y momento de par que actúa sobre el bloque rectangular por una llave. Especifique la magnitud de la fuerza y del momento de par de la llave, así como el punto donde su línea de acción interseca el plano x-y.
Respuesta
domingo, 10 de octubre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 22
4-138. Determine las magnitudes de FA y FB de modo que la fuerza resultante pase a través del punto O de la columna.
Respuesta
sábado, 9 de octubre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 21
4-137. Si FA = 7 kN y FB = 5 kN, represente el sistema de fuerzas que actúa sobre los voladizos mediante una fuerza resultante y especifique su ubicación sobre el plano x-y.
Resultados
viernes, 8 de octubre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 20
*4-136. Reemplace el sistema de fuerzas paralelas que actúa sobre la placa por una fuerza resultante y especifique su ubicación sobre el plano x-z.
miércoles, 6 de octubre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 19
4-135. Si se requiere que la fuerza resultante actúe en el centro de la losa, determine la magnitud de las cargas de columna FA y FB así como la magnitud de la fuerza resultante.
martes, 28 de septiembre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 18
4-134. Si FA = 40 kN y FB = 35 kN, determine la magnitud de la fuerza resultante y especifique la ubicación de su punto de aplicación (x, y) sobre la losa.
Respuesta
viernes, 24 de septiembre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 17
4-133. Las tres fuerzas paralelas de atornillado actúan sobre la placa circular. Si la fuerza en A tiene una magnitud de FA = 200 lb, determine las magnitudes de FB y FC de manera que la fuerza resultante FR del sistema tenga una línea de acción que coincida con el eje y. Sugerencia: se requiere que ∑Mx = 0 y ∑Mz = 0.
Respuesta
miércoles, 22 de septiembre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 16
*4-132. Tres fuerzas paralelas de atornillado actúan sobre la placa circular. Determine la fuerza resultante y especifique su ubicación (x, y) sobre la placa. FA = 200 lb, FB = 100 lb y FC = 400 lb.
miércoles, 15 de septiembre de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 15
4.131. El ducto soporta las cuatro fuerzas paralelas.
Determine las magnitudes de las fuerzas FC y FD que actúan en C y D de manera que la fuerza resultante equivalente al sistema de fuerzas actúe a través del punto medio O del ducto.
jueves, 26 de agosto de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 14
4-130. La losa de un edificio está sometida a cuatro cargas de columnas paralelas. Determine la fuerza resultante equivalente y especifique su ubicación (x, y) sobre la losa. Considere que F1 = 20 kN y F2 = 50 kN.
Respúesta
viernes, 20 de agosto de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 13
4-129. La losa de un edificio está sometida a cuatro cargas de columnas paralelas. Determine la fuerza resultante equivalente y especifique su ubicación (x, y) sobre la losa. Considere que F1 = 30 kN y F2 = 40 kN.
Respuesta
domingo, 15 de agosto de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 12
*4-128. Reemplace el sistema de fuerzas que actúa sobre el poste por una fuerza resultante y especifique el punto, medido desde el punto B, donde su línea de acción interseca al poste AB.
jueves, 12 de agosto de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 11
4-127. Reemplace el sistema de fuerzas que actúa sobre el poste por una fuerza resultante y especifique el punto, medido desde el punto A, donde su línea de acción interseca al poste AB.
Respuesta
lunes, 2 de agosto de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 10
Respuesta
jueves, 8 de julio de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 9
Respuesta
domingo, 4 de julio de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 8
martes, 1 de junio de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 7
Resultados
sábado, 8 de mayo de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 6
4-123. Reemplace el sistema de fuerza y par que actúa sobre el bastidor por una fuerza resultante equivalente y especifique el punto, medido desde B, donde la línea de acción de la resultante interseca al elemento BC.
Respuesta
viernes, 7 de mayo de 2021
SIMPLIFICACIÓN ADICIONAL DE UN SISTEMA DE FUERZA Y PAR - Problema 5
4-122. Reemplace el sistema de fuerza y par que actúa sobre el bastidor por una fuerza resultante equivalente y especifique el punto, medido desde A, donde la línea de acción de la resultante interseca al elemento AB.