CONCEPTO DE MOMENTO DE INERCIA - II

De este modo, el lector puede deducir que si la mayor parte del área se coloca lejos del eje centroidal, el momento de inercia tendrá a ser elevado. La fórmula matemática del momento de inercia, I, se desprende de la definición. Un método que se aproxima implica el proceso de sumatoria, indicando por

CONCEPTO DE MOMENTO DE INERCIA - I

En el estudio de la resistencia de materiales. la propiedad de momento de inercia es una indicación de la rigidez de una viga, es decir, resistencia a deflexionarse cuando se somete a cargas que tienden a flexionarla deflexión de una viga es inversamente proporcional al momento de inercia. 

Uso eficiente de material, colocar toda la materia alejado de eje centroidal que resulta práctico. Esta observación ser basa en la definición de momento de inercia que aquí se da

  El momento de inercia de un área con respecto a un eje particular se define como la suma de los proyectos obtenidos al multiplicar cada elemento infinitesimal de ella por el cuadro de su distancia

Centroide de formas complejas - III

Centroide de formas complejas - II

Éste se expresa matemáticamente como:

Centroide de formas complejas - I

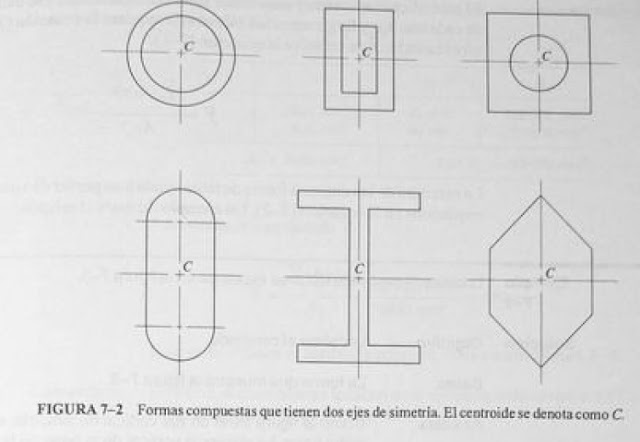
Se puede considerar que la mayoría de las formas complejas están compuestas de varias formas simples. Esto facilita la localización del centroide, como más delante se demostrará Otro concepto que ayuda en la localización de centroides es que si el área dispone de un eje simetría, el centroide se localizará en dicho eje. Algunas figuras complejas cuentan con dos ejes de simetría y por consiguiente, el centroide se localiza en la intersección de estos dos ejes En los casos en que no hay dos ejes de simetría, se usa el método de las áreas compuestas para localizar el centroide. Por ejemplo, considérese el área que ilustra la figura 7-3. Tiene un eje vertical de simetría pero no uno horizontal. Se considera que tales áreas se componen de dos o más áreas simples en las cuales se puede localizar el centroide aplicado el siguiente principio: 

Este principio utiliza el concepto de momento del área, es decir, el producto del área por la distancia de un eje de referencia al centroide del área. El principio establecer

Concepto de centroide – Formas simples

El centroide de una área es el punto respecto al cual el área se podría equilibrar soponiendo que se apoya en dicho punto. La palabra se deriva de centro y se puede considerar como el centro geométrico de un área. El en caso de cuerpos tridimensionales, el termino centro de gravedad o centro de masa se emplea para confundir. En el caso de áreas simples, tales como circulo, cuadrado, rectángulo y triángulo la ubicación del centroide es fácil de visualizar La figura 7-1 muestra las ubicaciones. 

Centroides y momentos de inercia de áreas

Objetivos

En capítulos anteriores se aprendió a determinar el valor de las fuerzas cortantes y momentos flexionantes en todos los puntos de vigas como fundamento para el cálculo de esfuerzos cortantes flexionantes de capítulos posteriores. Este capítulo continúa esta pauta al presentar las propiedades del perfil de la sección transversal de la viga, necesarias también para completar el análisis de esfuerzos y deformaciones de vigas. Las propiedades del área de la sección transversal de vigas que son de interés en este caso el controide y el momento de inercia con respecto al eje controidal. Algunos lectores ya han manejado estos temas gracias al estudio de la estática. 

Para ellos este capítulo constituirá un valioso repaso y una adaptación del tema a las aplicaciones de interés en la resistencia de materiales. Para aquellos que no han estudiado controides y momentos de inercia, los conceptos y las tecinas que se exponen en te capítulo les permitirán resolver los problemas de análisis de vigas incluidos en este libro y en muchas situaciones reales de diseño. Después de determinar el estudio de este capítulo, el lector será capaz de: 

1. Determinar controide 

2. Localizar el controide de formas simples por observación 

3. Calcular la localización del controide de formas complejas tratándose como compuestas por dos o más figuras simples 

 4. Analizar perfiles tic vigas compuestas integradas por dos o más perfiles estructurales estándar para determinar la localización del centroide y el momento de inercia resultantes. 

5. Reconocer que tipos de perfiles son eficientes en (unción de su capacidad de producir un gran momento de inercia en relación con la cantidad de área de su sección transversal.